Introduzione al Teorema di Bayes

Il Teorema di Bayes è uno strumento fondamentale nella teoria della probabilità che ci permette di aggiornare le nostre credenze sulla base di nuove informazioni. Esso fornisce un metodo per calcolare la probabilità di un evento, dato che si è verificato un altro evento correlato.
Probabilità Condizionata e Teorema di Bayes, Bayesian
La probabilità condizionata è la probabilità che un evento si verifichi, dato che un altro evento è già avvenuto. Il Teorema di Bayes ci fornisce un modo per calcolare la probabilità condizionata.
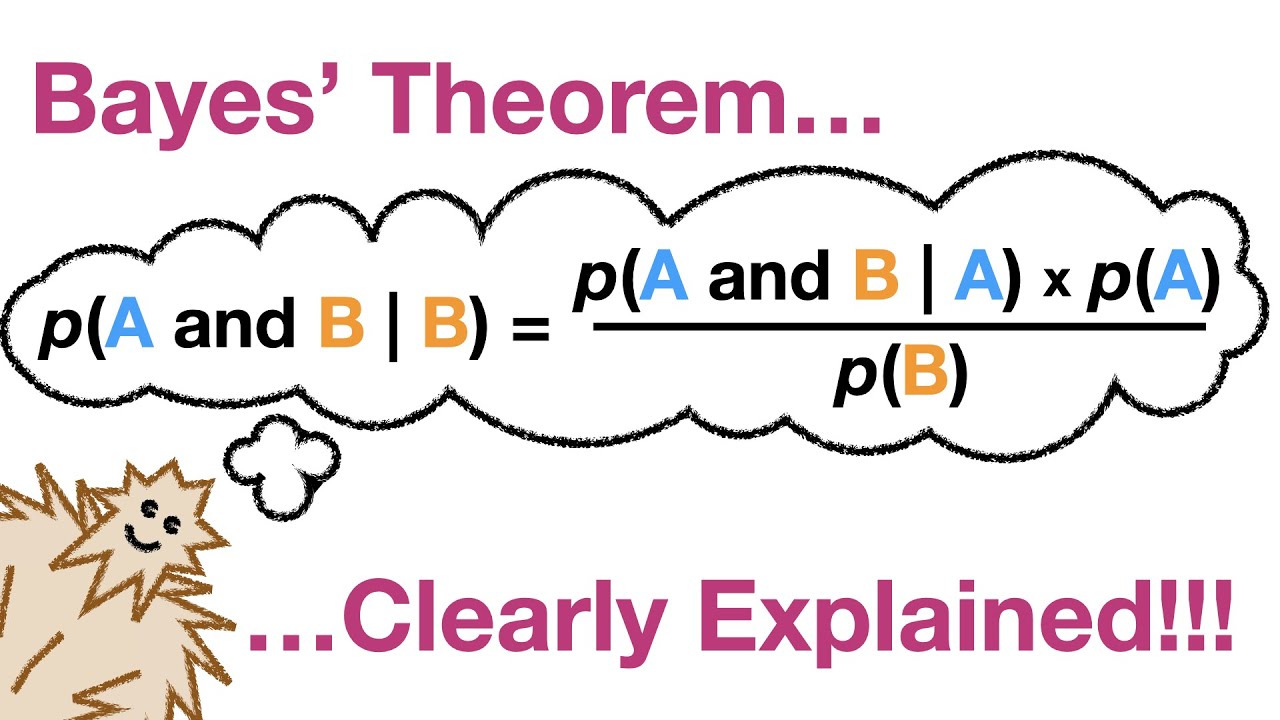
Il Teorema di Bayes afferma che la probabilità a posteriori di un evento A, dato che si è verificato un evento B, è uguale alla probabilità a priori di A moltiplicata per la verosimiglianza di B dato A, divisa per la probabilità a priori di B.
In termini matematici:
P(A|B) = [P(B|A) * P(A)] / P(B)
Dove:
* P(A|B) è la probabilità a posteriori di A dato B.
* P(B|A) è la verosimiglianza di B dato A.
* P(A) è la probabilità a priori di A.
* P(B) è la probabilità a priori di B.
Componenti Chiave del Teorema di Bayes
Il Teorema di Bayes si basa su tre componenti chiave:
- Probabilità a priori: La probabilità di un evento prima di osservare nuove informazioni. È la nostra conoscenza iniziale o credenza sull’evento.
- Probabilità di verosimiglianza: La probabilità di osservare nuove informazioni, dato che l’evento è vero. È la misura di quanto le nuove informazioni supportano l’evento.
- Probabilità a posteriori: La probabilità di un evento dopo aver osservato nuove informazioni. È la nostra credenza aggiornata sull’evento dopo aver considerato le nuove informazioni.
Esempio Pratico
Immaginiamo di avere un test medico per diagnosticare una malattia. Il test ha una sensibilità del 90%, il che significa che il 90% delle persone malate risulta positivo al test. Il test ha anche una specificità del 95%, il che significa che il 95% delle persone sane risulta negativo al test. Se una persona risulta positiva al test, qual è la probabilità che sia effettivamente malata?
Possiamo usare il Teorema di Bayes per rispondere a questa domanda. Assumiamo che la prevalenza della malattia nella popolazione sia del 1%.
* P(malato) = 0.01 (probabilità a priori di essere malato)
* P(sano) = 0.99 (probabilità a priori di essere sano)
* P(positivo|malato) = 0.9 (sensibilità del test)
* P(positivo|sano) = 0.05 (1 – specificità del test)
Utilizzando il Teorema di Bayes, possiamo calcolare la probabilità a posteriori di essere malato dato che si è risultato positivo al test:
P(malato|positivo) = [P(positivo|malato) * P(malato)] / [P(positivo|malato) * P(malato) + P(positivo|sano) * P(sano)]
P(malato|positivo) = [0.9 * 0.01] / [0.9 * 0.01 + 0.05 * 0.99] = 0.15
Quindi, la probabilità che una persona sia effettivamente malata, dato che ha risultato positivo al test, è del 15%. Questo esempio dimostra come il Teorema di Bayes può essere utilizzato per aggiornare le nostre credenze sulla base di nuove informazioni.
Applicazioni del Teorema di Bayes
Il teorema di Bayes, pur essendo un concetto matematico relativamente semplice, trova applicazione in un’ampia varietà di campi, dalla medicina all’ingegneria, dalla finanza all’intelligenza artificiale. La sua capacità di aggiornare le probabilità alla luce di nuove informazioni lo rende uno strumento potente per l’analisi e la previsione in contesti incerti.
Applicazioni in Medicina
Il teorema di Bayes è ampiamente utilizzato in medicina per la diagnosi delle malattie. Ad esempio, può essere utilizzato per calcolare la probabilità che un paziente abbia una particolare malattia, dato che ha presentato determinati sintomi.
- Consideriamo un test per una malattia che ha un’accuratezza del 95%, ovvero identifica correttamente il 95% dei pazienti malati e il 95% dei pazienti sani. Se un paziente risulta positivo al test, qual è la probabilità che abbia effettivamente la malattia?
- Il teorema di Bayes ci aiuta a rispondere a questa domanda, tenendo conto della prevalenza della malattia nella popolazione. Se la prevalenza della malattia è bassa, ad esempio dello 0,1%, la probabilità che il paziente abbia effettivamente la malattia, pur risultando positivo al test, potrebbe essere significativamente inferiore al 95%.
Il teorema di Bayes è anche utilizzato per valutare l’efficacia di nuovi trattamenti medici e per sviluppare sistemi di supporto alle decisioni cliniche.
Applicazioni in Ingegneria
In ingegneria, il teorema di Bayes viene utilizzato per l’analisi dei sistemi complessi, la previsione dei guasti e la progettazione di sistemi di controllo.
- Ad esempio, può essere utilizzato per prevedere la probabilità di guasto di un componente in un sistema complesso, dato che il sistema ha mostrato determinati sintomi di malfunzionamento.
- Questo aiuta gli ingegneri a prendere decisioni informate sulla manutenzione preventiva e sulla riparazione dei sistemi.
Applicazioni in Finanza
Nel campo della finanza, il teorema di Bayes è utilizzato per la valutazione dei rischi, la gestione del portafoglio e la previsione dei prezzi delle azioni.
- Ad esempio, può essere utilizzato per calcolare la probabilità di insolvenza di un’azienda, dato che ha presentato determinati dati finanziari negativi.
- Questo aiuta gli investitori a prendere decisioni informate sui loro investimenti.
Applicazioni nell’Intelligenza Artificiale
Il teorema di Bayes è un pilastro fondamentale dell’intelligenza artificiale, in particolare nell’apprendimento automatico e nella classificazione.
- Gli algoritmi di classificazione bayesiana sono utilizzati per prevedere la classe di appartenenza di un dato, ad esempio per identificare se un’immagine contiene un gatto o un cane.
- Questi algoritmi sono utilizzati in una vasta gamma di applicazioni, tra cui il riconoscimento facciale, la classificazione dei testi e la previsione del comportamento dei clienti.
Tabella Riepilogativa
| Applicazione | Esempio |
|---|---|
| Medicina | Calcolare la probabilità che un paziente abbia una particolare malattia, dato che ha presentato determinati sintomi. |
| Ingegneria | Prevedere la probabilità di guasto di un componente in un sistema complesso, dato che il sistema ha mostrato determinati sintomi di malfunzionamento. |
| Finanza | Calcolare la probabilità di insolvenza di un’azienda, dato che ha presentato determinati dati finanziari negativi. |
| Intelligenza Artificiale | Classificare un’immagine come contenente un gatto o un cane. |
Modelli Bayesiani
I modelli bayesiani sono una classe di modelli statistici che utilizzano il teorema di Bayes per aggiornare le credenze sulla base di nuove informazioni. Invece di cercare di stimare i parametri del modello in modo puntuale, i modelli bayesiani forniscono una distribuzione di probabilità per i parametri, che riflette l’incertezza associata alle nostre conoscenze.
Tipi di Modelli Bayesiani
I modelli bayesiani sono molto versatili e possono essere utilizzati per affrontare una vasta gamma di problemi di modellazione statistica. Alcuni dei tipi più comuni di modelli bayesiani includono:
- Modelli lineari bayesiani
- Modelli gerarchici bayesiani
- Reti bayesiane
Modelli Lineari Bayesiani
I modelli lineari bayesiani sono un’estensione dei modelli lineari tradizionali, che incorporano una distribuzione di probabilità sui parametri del modello. Questi modelli possono essere utilizzati per prevedere una variabile dipendente basata su una serie di variabili indipendenti, tenendo conto dell’incertezza associata ai parametri del modello.
Modelli Gerarchici Bayesiani
I modelli gerarchici bayesiani sono modelli che consentono di modellare la relazione tra più livelli di dati. Ad esempio, possiamo utilizzare un modello gerarchico bayesiano per modellare la relazione tra gli studenti, le loro classi e le loro scuole, tenendo conto della variabilità tra gli studenti all’interno di una stessa classe e tra le classi all’interno di una stessa scuola.
Reti Bayesiane
Le reti bayesiane sono modelli grafici che rappresentano le relazioni di dipendenza tra un insieme di variabili. Ogni nodo nella rete rappresenta una variabile, e gli archi rappresentano le relazioni di dipendenza tra le variabili. Le reti bayesiane possono essere utilizzate per inferire le probabilità di eventi non osservati, basandosi sulle probabilità di eventi osservati.
Vantaggi e Svantaggi dei Modelli Bayesiani
I modelli bayesiani offrono numerosi vantaggi rispetto ad altri metodi di modellazione statistica.
Vantaggi
- I modelli bayesiani consentono di incorporare informazioni precedenti sulla distribuzione dei parametri, il che può essere utile quando si hanno dati limitati.
- I modelli bayesiani forniscono una distribuzione di probabilità per i parametri, che riflette l’incertezza associata alle nostre conoscenze. Questo ci permette di quantificare l’incertezza nelle nostre previsioni.
- I modelli bayesiani sono relativamente facili da interpretare e possono essere utilizzati per generare previsioni affidabili.
Svantaggi
- I modelli bayesiani possono essere computazionalmente intensi, soprattutto quando si hanno molti parametri da stimare.
- La scelta della distribuzione a priori può influenzare i risultati dell’analisi.
- I modelli bayesiani possono essere difficili da costruire e validare.
Confronto tra i Modelli Bayesiani
I diversi tipi di modelli bayesiani hanno diverse caratteristiche in termini di complessità, flessibilità e applicabilità.
Complessità
I modelli lineari bayesiani sono generalmente meno complessi dei modelli gerarchici bayesiani e delle reti bayesiane. I modelli gerarchici bayesiani possono essere molto complessi, soprattutto quando si hanno molti livelli di dati. Le reti bayesiane possono essere molto complesse, soprattutto quando si hanno molte variabili.
Flessibilità
I modelli lineari bayesiani sono meno flessibili dei modelli gerarchici bayesiani e delle reti bayesiane. I modelli gerarchici bayesiani possono essere utilizzati per modellare una vasta gamma di relazioni tra dati, mentre le reti bayesiane possono essere utilizzate per modellare relazioni di dipendenza tra un insieme di variabili.
Applicabilità
I modelli lineari bayesiani sono adatti per modellare relazioni lineari tra variabili. I modelli gerarchici bayesiani sono adatti per modellare dati gerarchici, come ad esempio dati raccolti in più livelli. Le reti bayesiane sono adatte per modellare relazioni di dipendenza tra un insieme di variabili.
Bayesian methods are widely used in various fields, including finance, where they can be applied to analyze investment strategies. For instance, understanding the impact of investment decisions on market dynamics, as explored by invoke capital , can be enhanced through Bayesian frameworks.
By incorporating prior knowledge and updating beliefs based on new data, Bayesian models provide a robust approach to quantifying uncertainties and making informed decisions in the financial realm.
Bayesian methods, known for their ability to update beliefs based on new evidence, can be applied to the concept of autonomy. By incorporating individual preferences and experiences, Bayesian models can help individuals make informed decisions that align with their personal values and goals, fostering a sense of self-determination.
This approach can enhance autonomy by providing a framework for navigating complex choices and promoting self-directed action.
